质数与偶数的奥秘：探索数学中的基本概念

在数学的广阔天地里，质数和偶数是最基础且重要的数学概念之一，它们各自具有独特的定义和特性，对于数学研究、科学计算以及日常生活都有着深远的影响，本文将详细介绍什么是质数，什么是偶数，以及它们在各个领域的应用。

质数的定义与特性

质数，指的是在大于1的自然数中，除了1和它本身以外不再有其他因数的数，换句话说，一个大于1的数，如果只能被1和它自身整除，那么它就是质数，2、3、5、7、11等都是质数，质数具有许多独特的性质和应用。

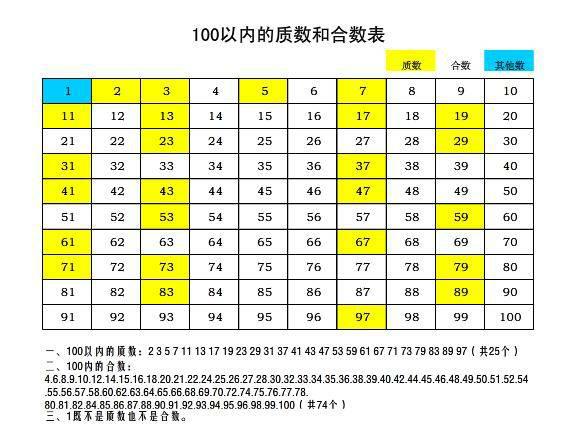
质数是构成密码学基础的重要元素，在网络安全领域，大质数分解的难度极高，使得质数成为加密算法的关键，质数在数论、几何学和物理学等领域都有广泛应用，质数还常常出现在日常生活中的各种场景，如电话区号的分配等。

偶数的定义与特性

偶数，指的是可以被2整除的整数，换句话说，如果一个整数除以2的余数为零，那么它就是偶数，偶数包括所有正整数和负整数，如2、4、-6、-8等，偶数具有许多独特的性质和应用。

偶数是构成数学中对称性的基础，在几何学中，许多对称图形都是由偶数性质推导出来的，偶数的概念在日常生活中无处不在，如日历中的日期、生活中的各种配对现象等，在计算机科学领域，偶数的概念也是实现算法和数据结构的基础。

质数与偶数的区别与联系

虽然质数和偶数都是数学中的重要概念，但它们之间存在明显的区别与联系，区别主要体现在定义和特性上：质数是指只能被1和它本身整除的大于1的自然数，而偶数是能被2整除的整数，联系则体现在它们的应用场景上：质数和偶数都在数学、科学计算以及日常生活中有着广泛的应用。

质数与偶数的应用实例

1、质数在密码学中的应用：质数是密码学中的关键元素，用于生成公钥和私钥，确保数据传输的安全性，RSA加密算法就依赖于大质数的使用。

2、质数在物理学中的应用：在粒子物理学中，质数的概念被用来描述粒子的质量谱和核结构，原子核的稳定性与质子数和中子数的质数性质有关。

3、偶数的对称性在数学中的应用：偶数的概念在数学中起着至关重要的作用，尤其是在几何学中，许多对称图形和图案的构造都依赖于偶数的性质，在计算机科学领域，偶数的概念也是实现算法和数据结构的基础，在计算机图形学中，旋转和缩放操作通常基于偶数性质来实现，在计算机编程中处理数据时也经常涉及到偶数的概念和应用，例如对数据的排序和筛选等任务中可能会涉及到偶数的判断和计算等任务，同时对于某些特定的算法和数据结构的设计也会涉及到对奇偶性的考虑和利用等等方面等等的应用场景等等的应用场景等等的应用场景等等的应用场景等等的应用场景等等的应用场景等等的应用场景等等的应用实例等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等等的应用实例等等的应用实例等等的应用实例等等的应用实例等等的应用实例等等的应用实例等也涉及到一些其他领域的应用实例比如统计学金融学和工程学等领域也会涉及到一些与质数和偶数相关的概念和知识比如统计学中的数据分析可能会涉及到数据的奇偶性分析以及利用质数进行数据处理等操作而金融学中涉及到的金融算法和金融模型也可能会涉及到一些与质数和偶数相关的知识比如利用质数进行加密保护金融数据的安全性和完整性等应用实例等等的应用实例等等的应用实例等等的应用实例等等的应用实例等等的应用实例等也体现了数学在其他领域的重要性和应用价值同时也体现了数学与其他学科的紧密联系和相互促进的关系总之无论是质数还是偶数都是数学中的重要概念它们在数学科学计算和日常生活等领域都有着广泛的应用通过学习和掌握这些概念我们可以更好地理解和应用数学知识为解决实际问题提供有力的支持同时也有助于拓宽我们的视野激发我们的想象力和创造力从而更好地适应现代社会的发展需求总之探索质数与偶数的奥秘不仅有助于我们深入理解数学概念还有助于我们在实际应用中发挥数学的价值和意义为我们的生活和工作带来更多的便利和创新让我们更好地运用数学知识解决实际问题更好地适应现代社会的发展需求更好地实现个人价值和社会价值的统一让我们共同探索这个充满奥秘的数学世界吧！